← Back to Portfolio

Autonomous Table Tennis Ball Collecting Robot

Mechatronics
Embedded C/C++
Control (P • PI)
Code ↗ Conclusions ↓

Abstract

This work details the design, modeling, control synthesis and experimental validation of two generations of an autonomous differential‑drive robot that detects and centers on a standard 40 mm table tennis ball. A progression from open‑loop servo actuation with proportional / PI guidance to cascaded PI regulation with DC motors and encoder feedback shifts the dominant performance bottleneck from actuation to perception. Sub‑centimeter steady‑state accuracy (≤0.5–1 cm) is achieved on static and slowly rolling targets while maintaining robust stability margins.

Contents

  1. Introduction
  2. Core Challenge
  3. Architecture Overview
  4. Prototype 1: Servo Platform
  5. Prototype 2: Encoders & Cascaded Control
  6. Prediction vs Measurement
  7. Minimal Arduino PI Loop
  8. Conclusions & Next Focus
  9. Portfolio FAQ

Key Contributions

Robot overview
Figure 1 — Autonomous robot prototype overview.

1. Introduction

Collecting dispersed table tennis balls between multi‑ball drills breaks training flow. Goal: an autonomous ground robot that rapidly detects, approaches, and centers on a (static or slow rolling) ball, emphasizing accuracy (≤1 cm), speed, and stability (low oscillation).

Development loop: Theory ⇄ Simulation ⇄ Experiment ⇄ Gap analysis ⇄ Improvement.

2. Core Challenge

Core challenge: Fast, precise, robust interception under variable lighting & friction, with constrained onboard compute.

3. Architecture Overview

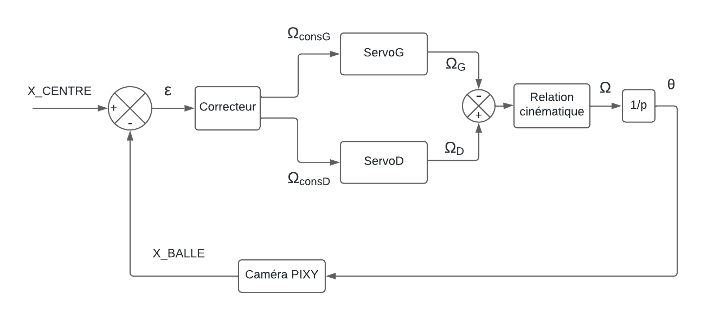
Prototype 1 architecture
Figure 2 — Prototype 1 architecture (servos, open loop speed).
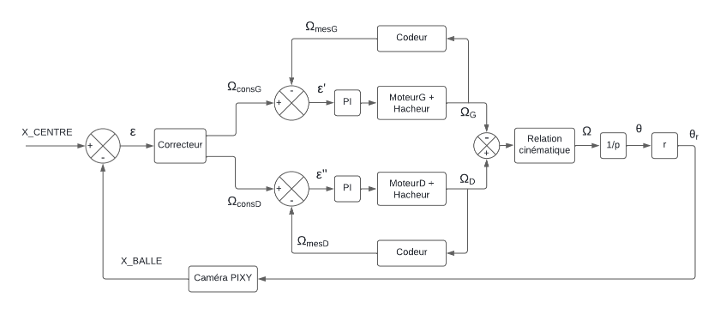
Prototype 2 architecture
Figure 3 — Prototype 2 architecture (DC motors + encoders + cascaded PI).

Figure insight (Fig.2–3) Prototype 1 applies the guidance law directly to servos with no wheel‑speed feedback → high sensitivity to servo asymmetry and battery voltage. Prototype 2 adds an inner PI speed loop (encoders) that linearises actuation so the guidance layer manipulates predictable differential speeds, reducing surface‑dependent response variance.

4. Prototype 1: Servo Platform

4.1 Hardware Stack

Prototype 1 hardware
Figure 4 — Prototype 1 hardware.

4.2 Vision Bearing Extraction

Processing chain: acquisition → HSV color mask → largest blob → centroid. Horizontal pixel offset becomes bearing error ε. Small‑angle approximation:

$$ \varepsilon \approx \frac{x_{px}-c_x}{f_x} $$Eq. 1 — Bearing error approximation
Optical guidance diagram
Figure 5 — Optical guidance flow.
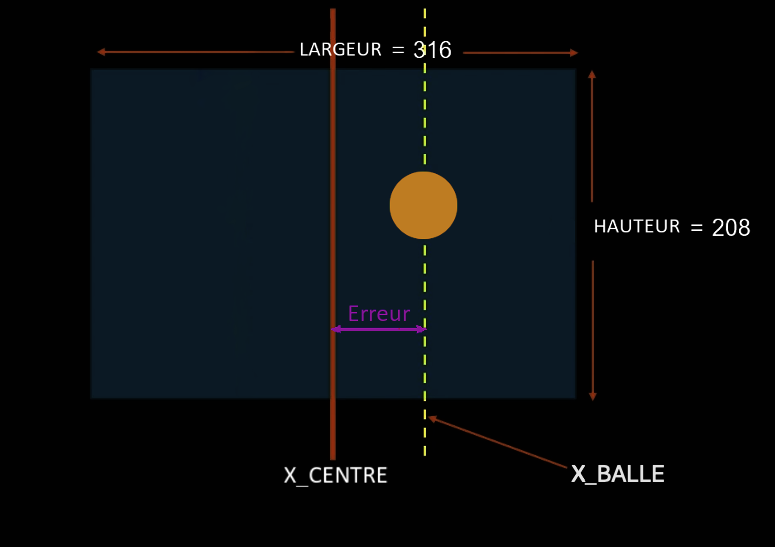
Camera principle
Figure 6 — Camera geometry.

Figure insight (Fig.5–6) The vision pipeline keeps only one blob centroid (robust vs clutter). The small‑angle approximation (Eq.1) maps horizontal pixel offset to a near‑linear bearing error—adequate bandwidth without heavy intrinsic calibration at this stage.

Design choice: keep vision minimal (latency & tunability) before richer perception (depth, learning).

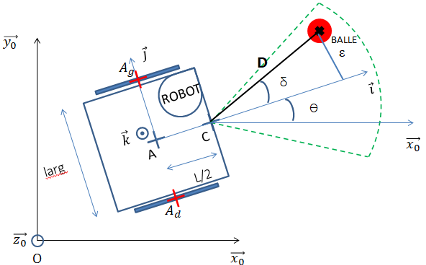
4.3 Kinematic Approximation

Differential drive (no‑slip, small heading error):

$$ \Omega = \frac{R}{L}(\Omega_d - \Omega_g) $$Eq. 2 — Differential drive relation

Used for preliminary gain sweeps (trajectory envelopes & steady‑state error sensitivity).

Kinematic simulation
Figure 7 — Simulated trajectory under P guidance.

4.4 Baseline P Guidance

Wheel command laws:

$$ \Omega_{\text{cmd D}} = \Omega_0 + K_p\,\varepsilon \qquad \Omega_{\text{cmd G}} = \Omega_0 - K_p\,\varepsilon $$Eq. 3 — Proportional guidance

Simulation looked stable → direct deployment.

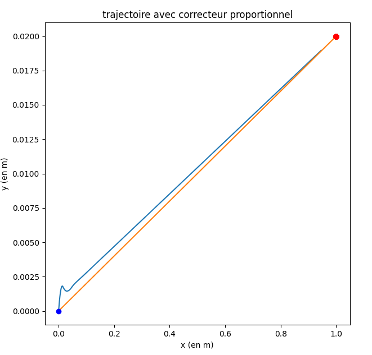
P controller theory
Figure 8 — P controller (theory).
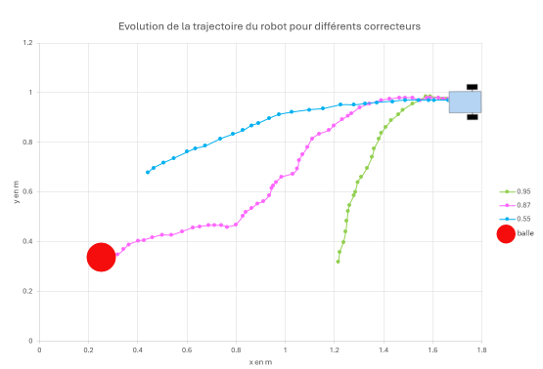
P controller experiment
Figure 9 — P controller (experiment) — oscillations from servo asymmetry.

Figure insight (Fig.8–9) Sustained oscillation stems from left/right speed imbalance: the proportional correction repeatedly overshoots because the effective wheel gains differ, injecting a persistent bias. Remedy: add integral action (slow compensation) or redesign actuation.

Limitations

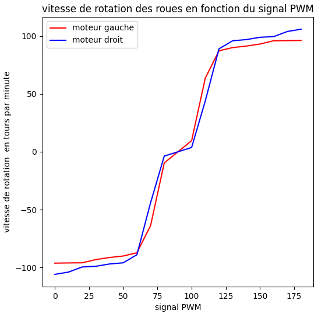
Servo asymmetry left
Figure 10a — Raw PWM step responses: left vs right servo actual speed (asymmetry visible).
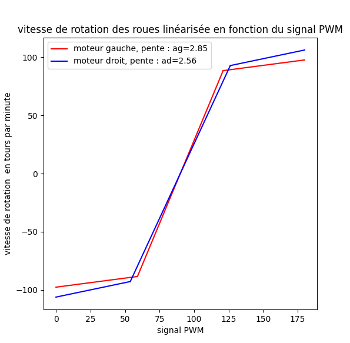
Servo asymmetry right
Figure 10b — Linearised (piecewise) speed model used inside simulation.
Experimental setup
Figure 11 — Instrumented test setup.

Figure insight (Fig.10–11) (10a) Empirical PWM→speed step responses show right servo higher effective gain (+12–15%) and a wider dead zone on the left. (10b) A simplified piecewise‑linear mapping substitutes the raw non‑linear curves inside simulation to preserve bias magnitude while enabling faster analytical gain sweeps. (11) Instrumented rig ensured repeatable capture of the asymmetric dynamics. This structural mismatch drives steady‑state offset under pure P; integral cancels it but increases time in saturation.

Clear unequal speed curves → biased steering & sustained oscillation. Hardware change justified.

4.5 PI Enhancement

PI guidance controller:

$$ C(p)=K_p + \frac{K_i}{p} $$Eq. 4 — PI controller form

Integral removed residual error at cost of hitting servo speed ceiling.

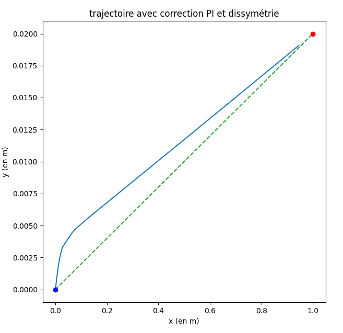
PI theory
Figure 12 — PI theoretical trajectory.
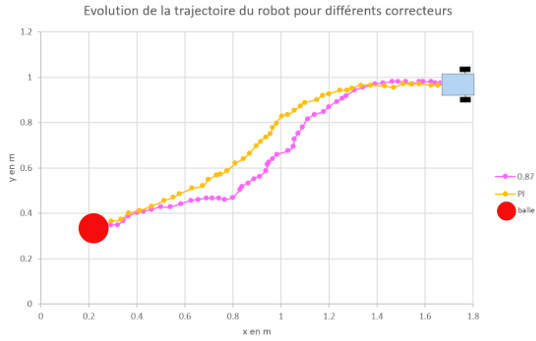
P vs PI experiment
Figure 13 — P vs PI experimental comparison.
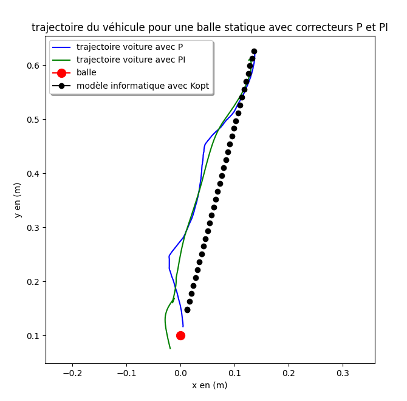
Static ball comparison
Figure 14 — Static ball: P vs PI vs theory.
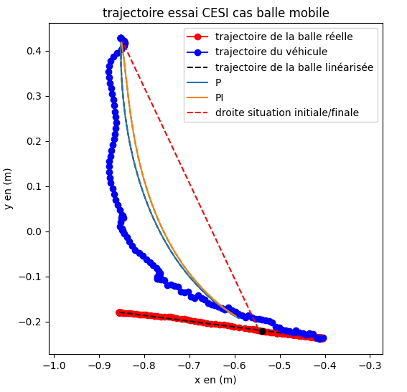
Moving ball comparison
Figure 15 — Moving ball comparison.

Figure insight (Fig.12–15) Integral action cancels bias but enlarges the initial saturation interval (command pinned at servo max), slightly extending capture time. The precision vs speed trade now hits the actuator physics ceiling, justifying the hardware redesign.

Findings: error ≤ 0.5 cm; performance now limited by servo saturation & mechanical asymmetry → redesign.

5. Prototype 2: Encoders & Cascaded Control

5.1 Redesign Rationale

Address saturation, asymmetry, and limited camera performance. Shift to a cascaded architecture decoupling velocity regulation from outer guidance.

5.2 Actuation & Sensing

DC motor
Figure 16 — DC motor + gearbox.
Encoders
Figure 17 — Incremental encoders.
H-bridge driver
Figure 18 — H‑bridge driver.

Result: guidance loop outputs target differential speeds instead of raw PWM → portability to battery & surface variation.

5.3 Motor Model

Step response identification → first order model:

$$ G(p)=\frac{K_m}{1+T_0 p}, \quad K_m=4,\;T_0=35\,\text{ms} $$Eq. 5 — Identified motor model

Parameters via least squares fit.

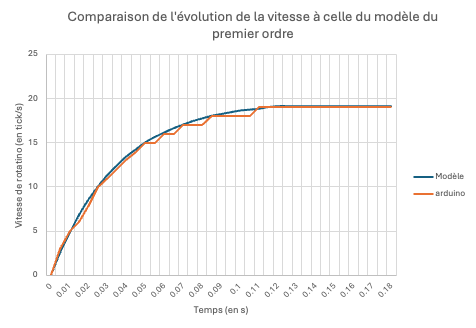
Measured vs model speed
Figure 19 — Model fit vs measured.

Figure insight (Fig.19) Residual error max < 5% over the operating band → first‑order model sufficient for the speed loop whose goal is mainly slow disturbance rejection (voltage, friction). No immediate derivative term needed.

5.4 Speed Loop PI

Speed loop tuning in PySyLic:

$$ K_p=44, \qquad T_i=0.17\,\text{s} $$Eq. 6 — Speed PI parameters

Target margins (30 dB / 45°) surpassed by measured (∞ / 66°) → strong robustness.

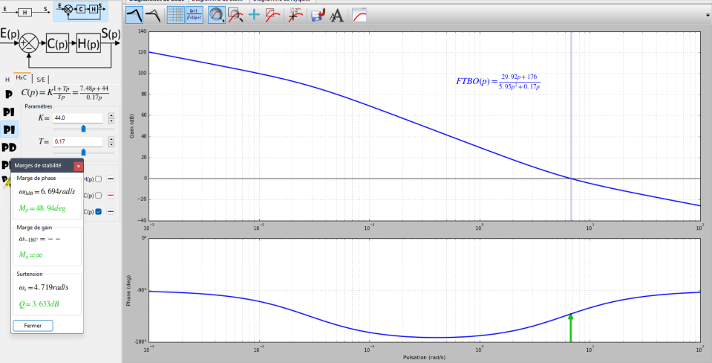
PI tuning
Figure 20 — PI tuning workspace.

Figure insight (Fig.20) Design tool reports 66° phase margin (> target 45°) giving robustness to friction variability + vision latency (tens of ms). Infinite gain margin (no crossover) signals low risk of destabilising noise amplification.

Inner loop shields outer guidance from motor & voltage variation.

5.5 Comparative Results

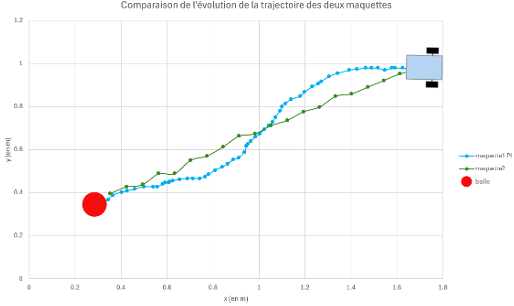
P1 vs P2 trajectories
Figure 21 — P1 vs P2 trajectories.
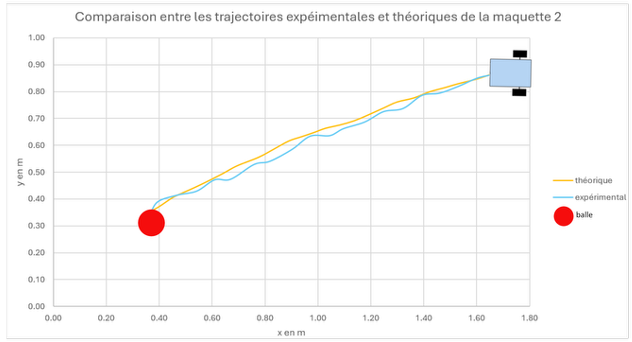
Static ball nonlinear
Figure 22 — Static ball: nonlinear theory vs experiment.
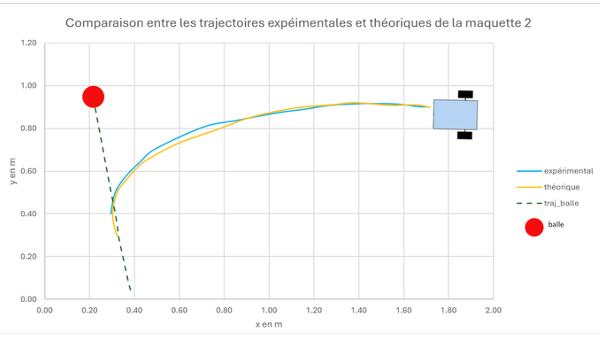
Moving ball nonlinear
Figure 23 — Moving ball: nonlinear theory vs experiment.

Figure insight (Fig.21–23) Prototype 2 both shortens capture time and eliminates terminal oscillation. Remaining model vs experiment gaps come mainly from perception latency + speed discretisation; qualitative dynamics (damping, low overshoot) match, validating the model → controller → hardware pipeline.

Bottleneck migrated: now vision frame rate & lighting noise, not actuation. Classic maturation signal.

6. Prediction vs Measurement

StageModel predictionRealityGapAction
P / servosFaster, residual errorOscillations ↑Servo asymmetryAdd integral
PI / servosError removedSpeed cappedSaturationDC motors + encoders
PI / DC motorsStable & fasterConfirmedVision noisePlan perception upgrade

7. Minimal Arduino PI Loop

arduino / motor_pi_control.cpp
// Encoder reading
  int ticksG = readEncoderG();
  int ticksD = readEncoderD();

  // Speed computation
  float omegaG = ticksG / T_sample;
  float omegaD = ticksD / T_sample;

  // Error
  float eG = omegaG_ref - omegaG;
  float eD = omegaD_ref - omegaD;

  // PI control
  uG += Kp * (eG - eG_prev) + Ki * eG * T_sample;
  uD += Kp * (eD - eD_prev) + Ki * eD * T_sample;

  // Saturation
  uG = constrain(uG, 0, 255);
  uD = constrain(uD, 0, 255);

  // Apply PWM
  analogWrite(motorG, uG);
  analogWrite(motorD, uD);

  // Save errors
  eG_prev = eG;
  eD_prev = eD;

8. Conclusions & Next Focus

Conclusions

Limitations

Future Improvements

9. Portfolio FAQ

Why switch from hobby servos to DC motors + encoders instead of “better servos”?

Instrumentation exposed persistent gain & dead‑zone asymmetry; moving to encoders + DC motors converted hidden bias into measurable states the controller can regulate.

Hook: steady‑state bias ≈ 0 cm; rare retunes.

How was the motor model identified & used?

Recorded step data → least‑squares first‑order fit → analytical PI tuning meeting target margins before hardware deployment, avoiding trial‑and‑error gain hunts.

Hook: first hardware test matched 66° phase margin design.

What is the next performance lever?

Perception latency & noise now dominate; roadmap: faster capture/processing, illumination normalization, optional lightweight depth to anticipate motion.

Hook: capture time reductions now vision‑bound.

© 2025 Marc Duboc — Plain HTML/CSS. Back to top ↑